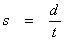 .
. Return to 2009 Insurgent Science Series home page.
Michael Augros
Presented January
28, 2009 at MIT on behalf of
The Institute for the Study of Nature
ADVERTISING BLURB: As Erwin Schrödinger wrote in 1951, “The isolated knowledge obtained by a group of specialists in a narrow field has in itself no value whatsoever, but only in its synthesis with all the rest of knowledge”. What could it mean to ‘synthesize’ all of natural science? To what extent is such a thing possible? Why is it desirable? Whose job is it? And how would it relate to mathematics? Come join Dr. Augros to explore the possibility of a general theory of nature.
SOME YEARS AGO I attended a lecture in which a respected scientist presented a very interesting thesis: No general theory can be of any scientific value. His argument ran like this:
As a corollary, he concluded that the modern synthesis of the Darwinian theory of evolution is of no scientific value. He took evolutionary science to be a sort of general theory, a grand synthesis which did not assist in making particular discoveries, and hence did nothing to advance our scientific understanding of the world.
I found these ideas rather shocking. But they started me thinking more seriously about the importance of general knowledge in science.
The more I thought about it, the more convinced I became that his second premise was false; general theories are useful and even necessary in making particular scientific discoveries. And though I agree with the scientist’s first premise, namely that every theory which is any good will have particular consequences, and will in some way assist in making particular discoveries, I don’t think that’s the whole value of a general theory.
If anything, the opposite seems to be truer. The intellectual value of particular discoveries seems to hinge on their connectivity with some more general or comprehensive understanding of the universe. A general theory of nature is a goal in science—a culmination of the scientific spirit that drives us to reduce many things to few, and few to one, as far as possible. One might say science was born of the desire to comprehend all things as the offspring of the smallest sufficient number of natural causes. Even if we go back as far as the ancient Greeks, to the first of the Pre-Socratic physicists, Thales of Miletus, we find that his attempt to understand the world was a kind of Theory Of Everything. All things are water, he said. Primitive as it sounds to us, that statement has been praised by many scientists for many reasons, not the least of them being that it revealed for the first time in history the scientific ideal: to understand all things through the smallest sufficient number of principles.
So what I want to do here is talk about the possibility and importance of a general science of nature. But right away I am forced to draw a distinction. There seem to be two kinds of general knowledge which we can have. One kind comes after our experience of all the particulars, and is a kind of unification theory, tying all the particular details together into one big picture. That kind of general knowledge has to be occasionally readjusted to fit with new particular findings. But another kind of general knowledge comes before our experience of particular things in all their details, and does not descend into the details, but remains at the general level. And that kind does not need to be adjusted in view of particular details, but rather the reverse: we must understand particular things in light of our more general concepts.
For example, we have to understand “plane figure” in general before we can define “heptadecagon” in particular. And that order of dependence goes only one way. We can understand what a “plane figure” is without understanding what a “heptadecagon” is. And we have to understand what a “chemical compound” is in general before we can understand what any particular compound is, but we don’t have to know what potassium aluminum sulfate is before we know what a chemical compound is.
So there seems to be a general type of knowledge of nature which is prior to our understanding of particulars. And since it is more necessary, and gets less talked about, I will focus my talk on that type.
Of course I can’t lay out an entire general science of nature in a lecture. But I can offer some indication of its existence and its importance. To do that, I’ll start by introducing a few distinctions[1] and definitions necessary for understanding what kind of general science I have in mind, and then the rest of the talk will consist of brief examples to give you a more concrete sense of it.
The first distinction I need to make is that between understanding the truth about reality, and making models of or hypotheses about reality.
Some scientists (particularly physicists) and certain philosophers of science will say that science is not about finding the truth. In science we do not really know that anything we are saying is the truth—in fact, we often know it is not the truth—but rather we just make models, that is, mental constructs which predict the phenomena, but which we have no reason to believe are faithful likenesses of genuine physical realities.
Certainly we have to be satisfied with that sort of thing in many cases. Often we can do no better than to construct models which we can’t verify definitively. And sometimes the best we can do is to make models which we know cannot possibly reflect what is really going on in nature, but which predict the phenomena with some degree of accuracy.
But that is not the ideal, nor is it all that science ever gets. For example, science has established that water is not an element, and no one is really worried that this view will someday be superseded. Today we think that in the normal process of human development, a zygote is first formed by the fusion of two microscopic gametes. No one lives in fear that this idea might turn out to have been a big mistake. Some things in science are secure, and represent a genuine knowledge of the truth.
Now for those whose scientific investigations aim at nothing but a model, not at truth, what I am going to talk about might have fairly little application. What I’m interested in talking about is when science is not just model-making, but claims real knowledge of the truth—a certainty about what is really going on in physical reality.
The next distinction I have to draw is that between general concepts and special concepts of nature. By ‘general concepts’ I will here mean not just any concepts which happen to be somehow more general than other ones, but I mean the most general concepts we can have of natural things. I mean any concept of what is found universally in all natural things, for example “whole,” “part,” “movement,” “change,” “existing in place,” “existing in time,” “cause,” “effect,” and many other such general kinds of things. And I call these concepts “general” for two reasons:
By contrast I call “special concepts” those which
For example, “aardvark” is a special concept, because it does not name something common to all things, but names a particular natural thing which one cannot know except by specific experience. And “mass” is also a special concept, even though it might be common to most or all things, since it is not a concept generally and automatically known to everybody, but must be introduced, and worked out by some special thought process. For example, it must be distinguished from “weight.” And not everyone has gone through that thought process.[2]
These two different kinds of concepts arise in different ways. Special concepts arise out of some special experience or else some special effort we make to observe or understand or explain something. General concepts are formed automatically by the human mind in response to common experience. (By “common experience” I just mean any kind of experience everyone has whether he likes it or not; the kind of experience we have of inevitable things such as “motion,” “rest,” “wholes,” “parts,” “one,” “many,” and the like.)
It should now be plain that there is an order of dependence here. Our special concepts depend on our general ones, and not vice versa. Take the concept of “instantaneous velocity.” This special concept involves general concepts which are more elementary, like motion, speed, and direction, and it can’t be understood without reference to them.
In a way, our general concepts are like natural materials. Certainly we can make artificial materials, but ultimately, since we have to start with something we didn’t make but simply found, and which nature provides, there must be natural materials in all our artificial ones. Our special scientific concepts of the world are like that. At bottom, they must involve our natural, elementary concepts which we do not invent or construct but which are just our automatic responses to immediate contact with reality. Such are the raw conceptual materials from which we must always begin, and which we can never simply discard and replace.
Now one last distinction I need to draw before advancing my thesis. Our general concepts are themselves of two types. Some are just simple concepts which make no assertion, but are the idea of some general kind of thing we all experience. For example, the simple ideas of “motion,” “time,” “size,” “shape,” and so on, which teachers assume we understand, and cannot really teach us, but can use, and presuppose in their definitions of more special concepts.
Other general concepts are affirmations or negations, basic and self-evident statements we all know to be true prior to all education. For instance, “Every motion has speed and direction,” or “Every motion takes time,” or “No infinite series can be traversed by going through it one step at a time,” and a host of other seemingly ho-hum truisms.[3] From this point on in the talk, I will be focused mainly on these kinds of “general concepts,” that is, basic statements which everyone knows to be true.
With these ideas in place, I can now state my thesis. Actually, I have two, but they are closely related. My first thesis is that (1) Our general concepts are causes of all our scientific knowledge and certainty about natural things. My second thesis is that (2) We can reason to a general, non-trivial knowledge of nature based on general concepts alone, without recourse to special forms of observation.
I am not saying general concepts are the only causes of our knowledge and certainty. For instance, if we study some species of animal, or the speed of light, we need much more than general concepts to have certainty about those particular things in their particularity. We need so much more, in fact, that we tend to lose sight of our dependence on general concepts at all. We need special concepts, special observations, special instruments, special forms of reasoning, and so on. And since all those take a great deal of effort, they get most of our attention, while general concepts, which come to everyone for free, tend to operate in our thought without our noticing them very much. They get lost in the details. Nonetheless, to the extent that natural science is not content with making models which might be no more than fictions, but claims to know or at least approach the truth about what is going on in nature, it must always bring our general concepts to bear on every particular result it derives.
So general concepts are not the only causes of scientific certainty. But they are causes of all scientific certainty, including the knowledge of the specialist. And that means our general knowledge is more certain than our special knowledge of nature. That surprises most people at first. What jumps to mind is that a general knowledge of something often leaves us uncertain, in doubt about more particular questions. For example, if I see something in the distance, I have a general knowledge that there is something there—but that alone leaves me in doubt about whether it is a living thing, whether it is a human being, whether it is my wife. Those more specific questions might not be answerable without more detailed observation. So people easily conclude that general knowledge is simply doubtful. But that’s unfair to general knowledge! General knowledge is knowledge of a general thing, not of a specific thing. So if we want to assess its certainty, we have to compare our certainty about general things to our certainty about specific things. For example, consider these two statements:
Statement (1) Some things move.
Statement (2) Light moves at 2.99792458 × 108 m/s.
Which is more specific? Plainly Statement (2), about the exact speed of light in particular. The statement that “Some things move” is far more general and vague and open-ended. But now which is more certain? Plainly Statement (1), which makes the humble assertion that some things move. We can be sure of the general statement about motion without being sure of the specific and precise statement about the motion of light, but we cannot possibly be sure of the specific statement about the motion of light without first being sure of the general statement about motion.
Now it is easy to think we don’t rely on generalities once we get down to specifics. So with my upcoming examples, first I want to highlight our dependence on general concepts when we claim to know specific natural laws, or when we claim to know something about nature as a result of specific scientific investigation.
It is also easy to think that general concepts, while necessary, in themselves are not sufficient to get us anywhere interesting or important. Starting just with our general concepts of nature, and without recourse to any special experience of nature such as measurement or experiment, it might seem we could never get beyond the boring, obvious statements everybody already knows without study or training. So I’ll offer a few examples to show that that’s not true.
My first example is Newton’s First Law of motion, which states (among other things) that if a body is in uniform motion in a straight line it will continue in that motion unless some new force is impressed upon it. Some people will say that this law is itself just a hypothesis, while others say it is a necessary truth and a certainty. Newton himself seemed to think it a known fact—he proposed it as a Law, not as a Postulate. But all I want to show is that we can’t know the law to be true unless we also know in advance certain general statements which are independent of the first law. Simply for the purposes of argument, then, I will assume that Newton’s first law is true and known with certainty.
Newton’s first law, incidentally, is not itself a general concept in the sense I defined earlier. It is not an idea which everyone automatically gets from ordinary experience. If anything, ordinary experience would incline us to think that things of themselves slow down and stop after a while. If we want to see the truth of Newton’s law, we have to perform a kind of mental abstraction from wind resistance, friction, and other things that slow a body down or curve its movement—a thought process not everyone has gone through. So in that sense, Newton’s first law is a special concept.
So if my thesis is right, it will be impossible to be sure of the truth of Newton’s first law without also being sure of the truth of some other statement about nature which is more generally known. And indeed that is the case. Consider, for example, the general concept that nature is regular or law-like. If we don’t already know that when we come to Newton’s first law, how can we know that Newton’s law applies to all bodies in effortless uniform motion in a straight line? And how can we know, simply by what we see a body doing in the present, what it will be doing in the future under similar conditions? Suppose you see someone sitting on a park bench at 9 o’clock. Can you infer that he will still be there at 10 o’clock, or a thousand years later, so long as nothing comes along and shoves him? No you can’t, since he can decide of his own accord to get up and go. In order to be sure of Newton’s first law, then, we must be sure that nature isn’t always like that—we must know that sometimes things move certain ways because they have to move that way, so long as nothing stops them. To become sure of the first law, we have need not only of specific experiences and thought processes, but we also need to have a more general understanding of nature; we need to know that there is a certain necessity and uniformity in the ways of nature.[4] Otherwise, we are left merely describing what we see in the present, with no certainty about what things will do later, whereas Newton’s first law is precisely about what things will do later.
Next I want to exemplify how the results or interpretations of specific experiments also depend on general concepts. My example is wave-particle duality. I mean the idea that both our particle models and our wave models of phenomena such as electrons are inadequate. Not everyone agrees on that—there is a significant minority of physicists who still hold to a particle-only model, and a smaller number who hold to a wave-only view. But suppose you think the infamous double-slit experiment really settles the matter, and demonstrates the inadequacy of either model for electrons. Are the specific results of the experiment the only data you rely on for your conclusion? No. You must also invoke a general concept about causation. The appearance of an interference pattern on a fluorescent screen is a separate event, after all, from the firing of electrons, one at a time, from some device like a cathode ray tube. And it is not possible to track the electrons at every moment along their path without making them go through just one slit, so that no interference pattern arises. So how do we know the interference pattern has anything to do with the electrons at all? Suppose you thought there was no connection, or you doubted there was any. In that case, the double-slit experiment could not possibly demonstrate the inadequacy of the particle model, since the interference pattern is no longer an effect which the model can be expected to explain.
Of course we all think the model should be expected to explain it. Everyone agrees on that. And yet it is not just the observed facts by themselves which convince us that the electrons cause the pattern; we don’t observe the electrons continuously from their emission to their striking the screen. We don’t “watch them striking the screen.” We infer they are doing so since the little flashes (which form the interference pattern) always show up when we do the experiment. We think we are justified, in other words, in thinking that when two natural phenomena are such that one always follows after the other, and there is nothing which is causing both of them, then the first of them is causing the second. So the firing of electrons and the interference pattern must be connected as cause and effect.
Certainly the conclusion that the particle model is inadequate depends on many special concepts, and on a special apparatus, and on special observations. And these are the main issue, and the real genius behind the conclusion. But it also depends on general concepts, such as the one mentioned about causation. We hardly notice our invocation of such a principle, since it “goes without saying,” it is so obvious. We nevertheless depend on that general principle if we are going to say we know something about electrons as a result of the experiment. And that general principle is quite independent of the results of the experiment; instead it is brought to bear on the experiment as a means of understanding it.
Now, my thesis is not just that general concepts are useful and necessary throughout the study of nature, but also that there is a general science of nature which can proceed in the light of general concepts without the need of any further experience of nature. It would be easy to think that we can’t get anywhere interesting or important with our general concepts alone, or that we must always use them together with, say, some special observation, if we want to get beyond the boring generalities which everybody already knows.
To show that this is not true, I’ll provide some illustration to the contrary. I’ll start with a demonstration of something which not everyone knows, which is even somewhat counterintuitive, but which depends on general concepts, and hence on the general experience which gives rise to them, but requires no further kind of experience of natural things.
The theorem has to do with uniform acceleration. We are used to defining uniform acceleration as motion in which the speeds acquired are proportional to the times elapsed. But why has it been defined that way? Why make the speeds proportional to the times rather than to the distances traversed? After all, if a body is speeding up, then the farther it goes, the faster it is going, right? So why not say the speeds it acquires are proportional to the distances it has traversed? Why doesn’t anyone talk about that kind of uniform acceleration?
The answer, which is surprising to many people, is that such acceleration is absolutely impossible. Here is the proof:
THEOREM: IN ANY MOTION FROM REST,
SPEED CANNOT BE PROPORTIONAL TO DISTANCE.
If possible, suppose a body is uniformly accelerated from rest such that its speeds are always proportional to the distances it has traversed. Let it traverse a distance d with a final speed of s.
Let 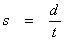 .
.
Thus a body traveling constantly at speed s would take time t to traverse d , and so in time t the accelerated body will have traversed only part of d, say p.
And, by assumption, upon traversing p the accelerated body will have a
speed v
such that
![]() .
.
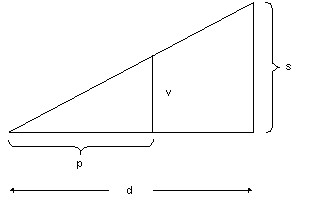 Hence
Hence
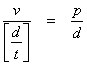
So
![]()
So
![]() .
.
Hence a body traveling at constant speed v will traverse p in time t.
But the accelerated body reaching a final speed v also traversed p in time t.
Which is impossible.
Therefore etc. Q.E.D.
Not earth-shattering, perhaps, but certainly not common knowledge. In fact, there was a time when Galileo himself mistakenly thought the opposite before becoming convinced. And, as promised, the argument made no reference to any experiment or special observation or measurement of any kind. And yet it is quite definitive. It makes use only of certain general concepts we all have about motion and speed and distance and the like, and a few basic statements about these things, as well as a little bit of elementary mathematics.
So, in the general science of nature I am talking about, although one begins only from things which everyone knows, and from experience which everyone has, one is not stuck simply saying things which everyone knows.
Now I’ve exemplified how specialized knowledge of nature depends on general concepts, and how general concepts can produce some interesting and exact results not known to everyone, even without the help of additional experience of nature. But this example about acceleration is admittedly still a fairly particular fact.
Can our general concepts provide us with general conclusions about nature that are not known to everyone? After all, I set out to talk about a general science of nature.
So my next example is meant to illustrate that, and it has to do with the continuity of motion. You are all more or less familiar with quantum physics, the physics of tiny discrete phenomena, but there is also such a thing as a physical consideration of the continuous, which one might call “continuum physics”. One theorem of the study of physical continua is this: Even though a motion is infinitely divisible, it is not an infinite multitude of successive locations of a body. It is tempting to try to conceive of motion that way. After all, a body has to pass through every place between its starting place and its stopping place. So why not understand motion as an infinity of successive locations of a body?
The reason is that on that understanding of motion, Zeno’s first motion paradox successfully proves the impossibility of motion. Consider that a body, to go from A to B, must first traverse half the distance, then half the remaining distance and so on. Since the motion, like the distance itself, is infinitely divisible, the body must first get ½ way to B, then ¾ the way to B, then ⅞ the way to B, and so on ad infinitum. For a body to finish any motion, however short, it must complete this infinite series. But that’s impossible. This isn’t because one doesn’t have enough time—it’s simply because it involves a contradiction to start and then finish going through an infinity of things one by one.
So long as we understand a finite motion as an infinite set of successive locations for a body, there must be a last member of the set, and in that last moment of motion, the body must complete the infinite series of reaching half-way points. And hence there will be a last term in that infinite series—which is simply an impossibility.
We are therefore left with a choice—either deny the existence of motion, as Zeno was crazy enough to do, or deny that motion is a multitude of events at all. It is rather one, single, continuous event. In a similar way, although it is a useful fiction to refer to a straight line as ‘an infinite set of points,’ the line cannot actually be a set of points. If the continuity of a line were constituted of its points, then its points would have to be in contact with each other, or right next to each other. Otherwise we would have gaps and not continuity. But points cannot be in contact with each other except by wholly coinciding, which leaves us just with a point, and not with anything that has locally distinct parts, like a line has. So a line can’t be composed of points by their being in contact. But neither can its points be right next to each other. That would mean that between two points there was no other point—but between any two distinct points there are always more points. So a line’s points can be neither in contact with each other, nor right next to each other. And therefore there is no way for the continuity of a line to arise from its points. A line, then, is not actually a set of points. It is another thing altogether, a length, which is divisible anywhere you like, as often as you like, but the points are not really there until they are introduced into the continuum by some act of division or termination.
Likewise a motion is a single continuous thing, not an infinite multitude of things. Although we can divide it at indivisible moments, as we can divide a line at indivisible points, it’s a mistake to think that the continuous is made up of the indivisible things that can divide it, as though the divisions were there already. It is the continuous thing that is fundamental, and the indivisibles which divide it do not fully exist until they are introduced into the continuous thing by some kind of division.
On this view of motion, there need be no last instant of motion at all, but only a first instant of rest—and hence Zeno’s motion paradox fails.
One can begin to see, from this example, how our general concepts of nature implicitly contain a body of conclusions which constitute an extremely general theory of nature. My final example is also very general, and concerns the definition of nature itself.
It is obviously not the job of any particular specialist to define “nature.” Hence we rarely see so much as an attempt to define the term, since everyone must be a specialist.[5] But can we really just ignore or discard the term? There is a major science journal called Nature. And “physics” takes its name from the Greek word for “nature.” And we speak of “laws of nature.” And all the sciences together are called “natural science.” It seems we cannot really understand the subject matter of natural science without understanding what is meant by “nature”.
It stands to reason that so general a concept should be definable in some way without reference to special concepts or observations, but just in light of general concepts and the givens of common experience. One place to begin is with the meaning of “nature” in typical usage.
One meaning of “nature” is synonymous with “the natural world” or “the universe.” We go for a walk out in “nature,” or we study “all of nature.” But that is obviously a derivative sense of the word “nature”. In a similar way, we sometimes use the word “life” to mean a whole world of living things, as when we say marine biologists explore “life” in the ocean. But as there can be no world called “life” unless there are many living things each with a life of its own, so there can be no world called “nature” unless there are many natural things each with a nature of its own.
So what does “nature” mean in the case of a single natural thing which “has a nature”? When doctors say they have done all they can do for their patient, and now they must let “nature” take its course, what do they mean by “nature”? Surely they don’t mean they will let the universe take its course. They mean that they will step back and let some principle within the patient do its thing, and see whether it can restore the patient to health.
So “nature” seems to mean a principle or cause of some change, but a principle or cause which is within the very subject of that change, not outside it. The doctor is a cause outside the patient who can make the patient get well. But “nature” means a cause within the patient.
True, but hardly a definition yet. After all, suppose a doctor heals herself by her knowledge of the art of medicine. Then her knowledge is a principle of her getting well, and that principle is within her, within the subject of the change from sickness to health. So: is her knowledge of medicine her “nature”? No. We tend rather to call it her “art”. Why? What’s the key difference?
One difference is that the knowledge of the art of medicine is something the doctor acquired over time. She was not born with it. But by ‘nature’ we tend to mean a principle that is first in a thing, there from the get-go, something inborn. Hence the word “nature” comes from the Latin word for “birth,” which implies something present from the beginning or from the first. And the Greek word for nature, phusis, came from a word for “growth,” implying a principle that is in a thing from its very genesis, and is responsible for all its growth.
Already we’ve distinguished “nature” from many sources of movement and change; it names not just any source of change, but an intrinsic and primary one. The world presents us with a mess of motions and changes to understand. Some things move because other things shove them. But ultimately, all motion must arise from things which have within them their own impulse to produce change, and in each thing of that kind there must be a first principle of motion. And “nature” designates that kind of principle.
Or almost. One further thought will help us see we need to add a slight qualification. Consider an artifact like a knife. It has an inner impulse of its own to move certain ways. For instance, if it is once put in uniform motion, it tends to stay in uniform motion of itself, unless interfered with by something outside. Should we say, then, that the knife has a nature, which is the first source within the knife of this tendency to remain in motion? Surely that’s a mistake. Although the knife has this tendency, it does not have it because it is a knife, but because it is made of some massy substance, or for some such reason. The fact that the massy substance is shaped like a knife for human purposes is beside the point, and is a mere coincidence.
With these distinctions in place, we can formulate a definition of “nature” thus: a nature is a first principle of a motion (or of changing or resting), existing within the thing to which that motion belongs as such (and not merely as a coincidence).
That there is such a thing as “nature”, thus defined, is obvious. There is motion and change in the world, and this fact arises from certain causes. But the things which are fundamentally responsible for the motions in the world have their own internal reasons why they behave in the specific and definite ways that they do—and among those internal principles, there must be foundational and primary principles, which is to say there must be natures.
But now the big question: what are the natures in the world? The order of questions here is analogous to the order of questions one must ask about the elements. The first thing to ask is what an “element” is: it means a kind of thing which can’t be chopped up into simpler kinds of things. From that definition and common experience alone, it is obvious that “elements” of some kind must exist. But it is another question to ask what the elementary things are, to identify them and recognize them. Is water an element? Or can it be chopped up into smaller things that are not water and are simpler than water? The definition of “element” by itself does not tell us.
That doesn’t make it a bad definition. It is not intended
as a “definition” in the sense of a set of criteria for testing what is and is
not an element, but simply for expressing what an element is. Similarly it is a
perfectly good definition of “prime number” to say An integer with no
integral factors less than itself except 1. And yet that definition alone
does not tell us whether the number
![]() is prime or not.
is prime or not.
Likewise for the definition of nature. We can be sure that “nature” exists in the world, since it means nothing else than the primary principles of motion inherent in certain things. But in which things? What are the things in the world that “have a nature”? We have seen that a knife, as a knife, does not have a nature. Any inherent impulse to change that it has belongs to it in virtue of something other than and prior to its being a knife.
Or what about a horse-and-buggy and its driver? That collection of things certainly moves on its own, and has principles of motion within itself, and yet it is not a thing with a nature of its own. It is not even really a “thing.” It is a group of things interacting with each other, and all its impulses to movement as a group are nothing more than net results of the impulses of its individual constituents interacting with each other. To speak of the “nature” of a horse-and-buggy, then, would be a mistake. The whole does not have a nature, but only its parts have natures. Much the same must be said of a mousetrap, or an automobile. Occam’s Razor should prevent us from attributing a special new “nature” to each and every phenomenon which moves and has a name. We should posit the least number of natures needed in order to explain all the phenomena.
So the temptation arises to attribute “natures” only to the elementary particles. These certainly have a kind of priority to everything else, and seem to have inherent principles of moving about in certain ways. And they are the elementary constituents of all other things. So why not say only these have natures of their own, while all macroscopic things are really just aggregates of them? A dog, for instance, would not really have a nature of its own, but it would be a collection of more basic things each of which has a nature. A dog would be, in other words, nothing else than a very complicated mousetrap, whose actions are due entirely to the natures of its materials, and not to some “nature” of the whole dog.
But one can see that there is something inadequate about this view, just from general concepts and the data of ordinary experience.[6] Of course it often happens that components by their interaction produce new behaviors which none of them has in isolation. While no part of a mousetrap by itself can trap a mouse, the properties of each part fully explain the net activity of the whole trap. But other times mere interaction of certain components cannot explain the net action, unless the natures of the components themselves be altered. This happens when a whole new reason for action is introduced.[7] Where there is a new kind of reason for action, there is a new kind of agent at work. For example, imagine any number of individuals who don’t care about the environment, but only about their own convenience. Can concern for the environment ever be a reason for their net action? They might interact in a way that happens to preserve the environment, but so long as we suppose the individuals act solely with a view to their own convenience, there can be as many of them as we like, interacting in any way we like, but no genuine concern for the environment will ever be the reason behind their net action. Therefore where we find action which really is done for the sake of the environment, a cause is at work other than the individuals described, or else the individuals themselves have changed their underlying motives.
Now, consider the ultimate elementary particles (or forces or fields or what have you)—whatever they may be, presumably they are blind, mindless things, obeying their own natural laws quite unconsciously and automatically. The elementary things, when we observe them existing and acting on their own, do what they do regardless of rational concerns, and they must do so, in accord with a preset program of action. They obey laws such as Newton’s first law of motion, and do so without any rational object in view. Any net result which they fully explain will therefore be fully intelligible apart from introducing (for example) any concern for truth. So, where we find actions which are not fully understandable apart from rational motives, such actions are not purely and simply the result of irrational natures interacting irrationally.
This means that in the case of a human being, who is composed entirely out of parts with irrational natures, and yet behaves rationally and puts his parts to rational purposes, we must admit the presence of a new nature, a rational nature. This nature is not something alongside the particles themselves, like another particle, or a vitalistic force floating about in between the particles and telling them what to do—it is simply the single, new, shared nature of the particles themselves, while they exist in that human form. This general understanding explains both why human beings have motives for action which their components in isolation do not, and also why we do nothing without using our atoms.[8]
To remain consistent, we should say something similar about horses or dogs or cats. Although they don’t act for rational purposes in the same sense we do, nevertheless they act for the sake of pleasure and for the sake of avoiding pain, which is again a reason for action incommensurate with that of senseless atoms and their senseless interactions. Animals have new kinds of reasons for action which don’t belong to the natures of their particles in isolation. Those particles have a new kind of impulse to movement, and hence a new nature, when they are in such forms. (If something analogous may be said for plants or chemical compounds, the grounds will have to be somewhat different, as they do not obviously have any reasons for action which differ from those of their ultimate constituents.[9])
Of course it is non-controversial and boring to say that animals have properties which atoms do not. The point I’m trying to make goes beyond that. I’m saying that atoms have a new nature when they enter into certain kinds of composition, such as that of an animal. It’s certainly possible to have a mere mess of atoms and molecules, or a mechanical mixture, or even a system of them interacting, like proteins in some solution in a Petri dish. But it is also possible to combine things in such a way that they cede their individual natures and henceforth have their existence and their properties through a new underlying nature. Consider a linguistic analogy. It is possible to combine words in three ways: (1) In one way, you get a mere mess or list of random words, (2) In another way, you get an ordered system of interacting words, as in a descriptive phrase or a sentence, (3) And in still another way, you get a compound word. In the first two ways of combining words, either on a list or in a sentence, we continue to have many words. In the second way, we have one phrase or one sentence, but still many words. In the third way of combining words, in the compound word, we have only one word. Hence “blackbird” is composed of “black” and “bird,” and yet those component words have no meaning of their own insofar as they are parts of that new compound word. The phrase “black bird” is not synonymous with “blackbird.” “Blackbird” is a new beast, with a meaning of its own, though all its sound properties arise out of its components. In a similar sense, according to the argument I made on general principles and facts of ordinary experience, when elementary natures come together in certain ways, they sometimes form a single new nature, which replaces the several natures of its components and does the work of producing their old properties toward new objects, or with new meaning, you might say. We have reason to think something like this is going on in the case of an animal, for example. But in the case of an automobile, it is not acting for any purposes of its own, but its form is simply imposed on its materials from the outside, and all its so-called “purposes” are really our purposes, and are of no concern to it whatsoever. So nothing prevents us from saying there is nothing radically new in the automobile—it is just a bunch of natures interacting systematically, and there is nothing there with a brand new reason for action all its own. It is like a phrase or a sentence, which is still many words, although in a definite and unified arrangement.
In this way general experience and general concepts not only provide some answer to the question “What is a nature?”, but even offer some insight into the question “What things have natures of their own?” And while the side you take on this question might make little difference in your day-to-day work in a lab, it makes all the difference to what you think the natural world is.
It was my intention to give you some sense of the importance of general concepts in natural science, both in our particular investigations, and in the formation of a general understanding of nature.
If I had to give a name to such a general science, I would have to call it some kind of “physics,” because that is commonly regarded as the most basic and general of the natural sciences. We might call it “bigger” physics, to distinguish it from all the rest of physics, which takes a more specialized approach to things. As the principles and conclusions of chemistry underlie those of biology, but not vice versa, and the principles of physics underlie those of chemistry, but not vice versa, so the principles of the general physics I have been at pains to describe underlie all of natural science. So we might call it “fundamental physics.”
I have tried to bring out some characteristics of this “fundamental physics.” For example, although it is very elementary and thus uses only elementary mathematics (and usually uses none at all), it is nevertheless ‘more mathematical’ than the more specialized branches of natural science in its manner of thinking. What I mean is this. Mathematics reasons from self-evident principles without the need to consult further kinds of experience beyond those presupposed to its principles. What I am calling “fundamental physics” does the same. Other parts of natural science typically must have recourse to specialized observations, and very often do not use simple syllogistic deduction, but instead reason by induction or by affirming the consequent. Hence “fundamental physics,” the most general part of the science of nature, attains to a degree of certainty that borders on the mathematical, given its mode of reasoning and the kinds of experience and principles from which it begins, and given the mode of reasoning it employs.
Another characteristic of “fundamental physics” is that it is impossible to abstain from it entirely, thanks to its generality. Every specialist must do it, whether unconsciously and half-heartedly (and hence poorly), or deliberately and explicitly (and then there is a chance of doing it well). The danger of doing it unconsciously is that when we don’t explicitly learn and carefully examine the general principles which affect how we understand nature, it becomes easier for general assumptions to sneak into our thought and masquerade as self-evident truths. After all, many specious ideas occur to us quite effortlessly, and we easily mistake them for reliable self-evident concepts, when they are nothing of the kind. For example, many people, without special instruction, would consider it self-evident that -20° is “twice as cold” as -10°. Or, if we are prone to imagining that natural quantities behave just like mathematical ones, we might think it self-evident that there is no such thing as a greatest speed.
So what I’m calling “fundamental physics” is useful, to some extent necessary, and can be dangerous to ignore. Its main value, however, is not its affect on the various specializations, but in the general understanding of nature which it affords. In the blurb advertising this talk I quoted Schrödinger bemoaning the necessary evil of hyper-specialization. He said that specialized knowledge has no value apart from its synthesis with all other knowledge. I think he was right. At any rate, if the universe is a coherent and intelligible whole, like a portrait or a story, and not just a heap of things piled up at random, then an adequate appreciation of any one part would seem to depend upon a general sense of the whole. But no one can have a specialist’s knowledge of all the parts. In that regard, the fundamental physics I have been describing can serve to counteract somewhat our doom to mental myopia.
[1] Here I must acknowledge a debt to Marcus Berquist of Thomas Aquinas College, from whose 2001 lecture entitled “Common Conceptions and Proper Conceptions in the Study of Nature” I drew much inspiration for the substance of this talk, including my selection of examples. While my examples and vocabulary differ somewhat from his, and I do not wish any defects in this talk to be attributed to him, nevertheless I would be remiss not to mention his work as a source.
[2] Similarly, the idea of “motion” is a general concept, common to everyone. But the definition of motion which Aristotle gives in his Physics, although it is no more specific than motion itself, is nonetheless a specialized concept in the sense that not everyone has gone through the thought process required to understand the meaning of that definition, and to see that it does indeed express what motion is. Everyone has a general idea of “motion.” But not everyone has the idea of motion expressed in Aristotle’s definition. Similarly, everyone has an idea of “brave,” but this common idea is confused. Not everyone has a sound definition of “brave”, and some people don’t have any definition of it at all.
[3] Not every self-evident statement is a “ho-hum truism,” i.e. something actually known to everybody. For example, “No prime number is a perfect number” is self-evident, or very nearly so, to anyone who knows the definitions of “prime number” and “perfect number.” But not everybody knows those definitions.
[4] To use a more traditional language to say the same thing, one must recognize that nature is “determinata ad unum.” Natural causes, as natural, are not open to producing opposite effects in the way that rational agents, as rational, are. To say that nature operates in a definite way and cannot help it is not, then, the same thing as a ‘deterministic’ view of nature, if the latter is meant to exclude the existence of freewill. It is only to say that natural causes, as natural, are not free to do otherwise than they do.
[5] Perhaps people could be said to “specialize” in the general science of nature I am here describing, but there are few who do so today.
[6] There are in fact many givens of common experience by which one can see that a dog (or a horse or a man) cannot truly be a collection of natures. The principal way is through the unity of those activities traditionally called “immanent.” An “immanent” action, by contrast to a “transitive” one, is one that terminates in the agent (the subject of the action), rather than passing out of the agent and terminating in some object. For instance, “kicking” is a transitive action, since it begins in the kicker and ends in the thing kicked. But “seeing” is an immanent action, remaining within the one who is doing the seeing. Now where there is one transitive action, there might be many agents, since many agents can act on some single external object, as when many men draw a ship to shore, each pulling on different ropes or different parts of the same rope. In such a case, the unity of the action might be due to the object alone. But in the case of immanent actions, such as seeing, hearing, imagining, remembering, wishing, fearing, and understanding, where there is one action, there is one agent, and it is not possible for many distinct agents to contribute to a single action. Any individual human being, then, reflecting on his own immanent activities, has in his immediate experience a constant testimony to his individuality as an agent, i.e. to his “substantial unity”. But given the audience for whom this talk was first written, I thought it best not to go down that road.
[7] By a “reason for action” I mean an end for the sake of which action is done, and which is the motivation of the agent’s movement. One must recognize natures by natural motions, and natural motions by natural ends. So we can recognize the presence of a new nature where there is an end for the sake of which other natures cannot possibly be acting. Cf. Aristotle’s Parts of Animals 1.1 641b24 ff.
[8] I do not mean to say that human beings have no activities except those which they perform by means of their atoms, molecules, organs, and the like. But even though we do have such activities, we do not perform even those without dependence on the simultaneous use of our organs etc. We cannot think, for example, without brain activity, even if brain activity and thought are not identical.
[9] If the molecules of a plant are acting for the good of the plant, then indeed there is some new end for the sake of which action is being done. But it is more obscure that plants have a good and act for the sake of it than it is that animals do so. It is still more obscure that inanimate things, like water, have a “good” of their own, and “act for the sake of it.”
I add these appendices in connection with my fourth example, concerning Zeno’s paradox and the continuity of motion. In that example, I presumed the infinite divisibility of motion, to which someone might object—hence Appendix 1. Also, someone might think that the mere use of calculus is an adequate answer to Zeno’s motion paradox, so that there is no need to deny that a motion is a set of locations or moments—hence Appendix 2.
Some today would be willing to deny the infinite divisibility of motion and say, instead, that locomotion from A to B might consist in discrete successive momenta, which have only the appearance of continuity because of their small intervals and great rapidity. Motion might, in other words, be like a movie, in which there are many discrete frames, finite in number, which succeed one another very rapidly, and hence there is no true continuity of movement, but only an illusory one. This idea seems to enjoy more plausibility than it would otherwise in view of the strangeness of quantum phenomena, which often do not behave according to the rules which govern more macroscopic objects. If electric charge can be quantized, and matter can be quantized (even though it appears continuous to the eye), why can’t motion be quantized, too?
But this is a mistake. Certainly it is possible for discrete events to take place in rapid succession and assume the appearance of continuity, or of infinite divisibility. But when this occurs, there is no true motion, and there is a cause outside the discrete events, producing them by means of true motions (like the projection of an image by light, or the movement of a movie reel).
In the following demonstration of the infinite divisibility of motion, we must first know that distance is infinitely divisible, and that time is as well.
What would it mean for distance not to be infinitely divisible, but to be made up of a finite number of discrete indivisibles? Can a finite number of points make up a distance? Either they are separated by distances or they are not. If so, there are distances between them along which we may take more points, and so on to infinity—and hence distance is infinitely divisible after all. And if the points are not separated by any distances between them, then they coincide in a single point, which has no length or distance.
Hence distance is infinitely divisible, whether it be physical or mathematical.
So too time is infinitely divisible. For if we take any length of time, it must be divisible into past and future time by any indivisible “now” occurring in it. If it is not so divisible, it is not a length of time at all, but only a “now.” Can this length of time be made up of a finite number of discrete, indivisible “nows”? Either they are separated by lengths of time, or they are not. If so, there are lengths of time between them along which we may take more “nows,” and so on to infinity—and hence a length of time is infinitely divisible after all. And if the “nows” are not separated by any length of time between them, then they coincide in a single now, which has no duration at all, so that the length of time we started with is simply a “now.”
Hence any length of time is infinitely divisible.
Now consider the motion of a body from point A to point Z. Suppose, if possible, that the motion is not infinitely divisible, but instead consists in a finite number of locations of the body at A, then B, then C, and so on, up to Z.
Since the distance from A to Z is divisible to infinity, but the body (by our assumption) occupies only a finite number of locations between A and Z, therefore the body does not occupy every place between A and Z during its motion. Hence there are distances between its successive locations, distances over which it never travels. For instance, the body is first at A and next at B without every going through the places between A and B.
Now, either the body is at A and B at the same instant, or not. If so, one might say this is absurd in its own right, i.e. for the body to be in two places at once. But if the objector replies “It seems ‘absurd’ for the same body to be in two places at once only because you never see it at the macroscopic level; but who knows what happens at the microscopic level?”, then we may still reason to further consequences. Suppose the body is at A and B at the same instant, and likewise it is at B and C at the same instant, etc. Then the body is in all the places through which it moves all at the same instant, and hence the whole motion from A to Z will take no time. So if this is the nature of motion, even macroscopic motion will take no time. But every motion takes time.
Hence the body cannot be at every point in its motion at the same instant. But then it is at successive places in different instants, e.g. it is at A at one instant and at B at a later instant (for if this be not so in any one case, then the body is at all the places at the same instant, and motion takes no time, which is contrary to what we observe). But since time is infinitely divisible, and not composed of a finite number of indivisible “nows”, it follows that between the instant that the body is at A and the instant that the body is at B there must be some length of time that has elapsed (just as between any two distinct points along a line there must be some distance between them). Accordingly, there will be a time during which the body is not at A, not at B, and not at any of the points along its motion. Hence either it exists somewhere else, or it does not exist at all.
Here, some are willing to invent a fictional “other world” or “other dimension” in which the body can exist while it has disappeared from ours. There is no reason to believe in such a thing. One should reply, with Newton, “I will not feign hypotheses”.
But one could also say that on such a view there is no reason why the body should appear back in our world again at all, and certainly no reason it should keep reappearing at the next location along a definite path. Is that pure luck? If so, it should be rare, and then even macroscopic “motions” will consist for the most part in the haphazard locations of a body over time, which is contrary to experience. On the other hand, if one wishes to establish some rule or cause in this “other world” which governs the reappearance of the body back into our world according to definite rules, one is in effect inventing a “film projector” in another world to be the cause of the seeming continuity in ours. But then what is the nature of this “film projector”? Do its “motions” also consist in surprisingly orderly disappearances and reappearances? Then the explanation also requires explanation. If its “motions” and activities instead are infinitely divisible and genuinely continuous, then we have our result: true motion is infinitely divisible, but we are unfortunate enough to live in a fake world, not the real one.
In sum: if one denies the existence of infinitely divisible motion, it follows either that motion takes no time, or else that a body in motion spends time in other worlds (or out of existence altogether), and hence there is no reason why motion exhibits order. Since these consequences are unthinkable and contrary to the observed facts, so too is the idea that motion is discrete.
Hence motion is infinitely divisible. Q.E.D.
Some people answer Zeno’s first motion paradox (i.e. that a body must go half way, then half the remaining distance, etc. ad infinitum, and hence can never finish a motion) by saying that the body does not spend any time at any of the various points in its motion. Hence, although those points are infinite, it does not take an infinite time, but a finite one, to get somewhere.
That answer is inadequate. Zeno’s paradox is independent of how much time is spent at any given point. So long as the body is at those different points at different times, and so long as you grant that those points are infinite in multitude, and that the motion consists in being at those different points in succession, the motion will be impossible. For it will consist in running through an infinite series of things successively, which is impossible, since there must be a last term in the series (since the body supposedly finishes running through it), and yet there cannot be a last term in the series (since the series is given as endless and without a last).
Similarly, people think they have answered Zeno simply by saying that the integral of the series of traversed lengths is finite, even though the series of terms is infinite. What they say is true, but it is not an adequate answer to Zeno.
The idea of an “integral” was developed in the calculus precisely because it is not possible to add up an infinity of things, and yet it is often desirable to know whether there is something finite that an infinite series gets as close to as we like, though without ever getting there. Just as we don’t simply set h equal to zero in order to find the limit of
![[f(a+h)-f(a)]/h](Augros_2009-Bigger_Physics_files/image016.gif)
as h approaches zero, so too we don’t simply set n equal to infinity in order to find the limit of the series
![]()
Taking the integral means finding the limit, which does not mean setting n to infinity and adding it all up. That is impossible, and not just because of our time constraints. What we do instead is prove that the series converges on a definite quantity, namely 1, which the series never reaches. Although there are many quantities the series never reaches, 1 is a special quantity which the series never reaches, since it is the first quantity which the series does not reach. The series comes as close to being equal to 1 as you like, if you take n sufficiently large. We can make the sum of the series differ from 1 by less than any pre-assigned difference (e.g. one billionth, one trillionth, or whatever you like), so long as we take n large enough.
And it is easy for us to say, sloppily, “the sum of all is equal to 1.” But if we really care about understanding what we’re saying, we will say instead “The limit of the series is equal to 1,” precisely because the series itself can’t “get there.”
1 is not the last thing reached by the series. If it were, the series would have a last term. But it doesn’t. So there is no last thing it reaches. There is only a first thing it does not reach (i.e. 1)—and that, by itself, is simply making Zeno’s point, not refuting him.
Also available in PDF.
Return to 2009 Insurgent Science Series home page.